Abstract

Probability (P) of binomial event is a commonly estimated quantity in ecology. Recently, interest has moved to estimation and communication of the associated uncertainty about the estimates of P.

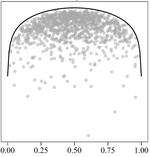
Here I use the principle of maximum entropy to introduce truncated exponential probability density function f(P) on a closed interval [0,1] that gives expectation of the uncertainty, given that the only information we have is a single-number estimate P_single, which I assume to represent mean μ of an unknown probability density distribution of P. This expectation puts an upper bound on the maximum uncertainty about P. I also present the associated cumulative distribution function, quantile function, and random number generator. I demonstrate the MaxEnt f(P) on a species distribution model predicting probability of a species’ occurrence on a geographic map. T

he MaxEnt f(P) presented here can be used to make conservative probabilistic statements about probability statements, and it can be used as an alternative to beta distribution, and as the least informative prior distribution of P in Bayesian modelling.